调制信号的振幅与频偏之间的关系,根据不同的调制方式(如幅度调制AM和频率调制FM)有所不同。在幅度调制(AM)中,载波的振幅随着调制信号的变化而变化,但其频率保持不变。这意味着,如果调制信号的振幅增加,那么通过AM调制得到的已调波的振幅也会相应增加,但这并不直接影响频偏。
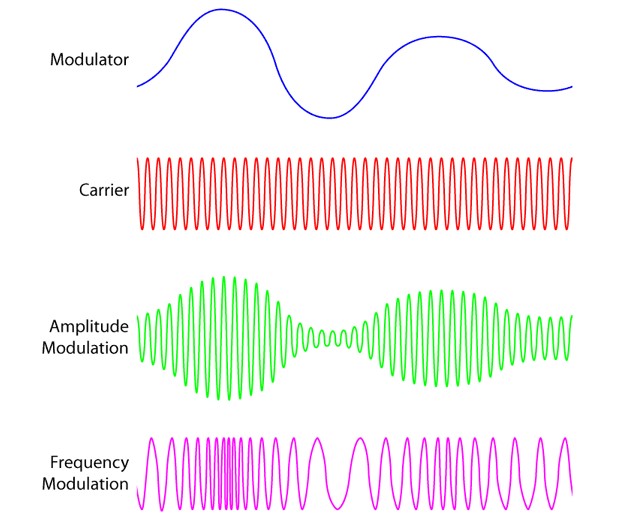
对于频率调制(FM),情况则不同。在FM中,载波的频率随着调制信号的变化而变化,而其振幅保持不变。在这种情况下,调制信号的振幅越大,调制后的波形偏离载频频率的程度越大,即频偏就越大。这表明,在FM调制中,调制信号的振幅与频偏之间存在直接的关系,且这种关系在小信号情况下是线性的。
对于幅度调制(AM),调制信号的振幅主要影响已调波的振幅,而不直接影响频偏;而对于频率调制(FM),调制信号的振幅直接影响频偏,且在小信号情况下这种关系是线性的。
一、 调制信号振幅对频率调制(FM)频偏影响的数学模型是什么?
调制信号振幅对频率调制(FM)频偏的影响可以通过数学模型来描述。我们知道FM调制是一种使载波的频率随调制信号的大小变化而变化,而振幅保持不变的调制方式。这意味着在FM调制中,基带信号的信息是通过频率的变化来承载的。具体到数学模型,虽然直接的公式没有在证据中给出,但我们可以根据描述推断出频偏与调制信号振幅之间存在线性关系。
更进一步地,证据表明最大频偏是调制指数的一个决定因素,且调频的频偏和调制信号的幅度成线性关系。这说明了调制信号的振幅如何直接影响FM信号的最大频偏。因此,可以推断出一个简化的数学模型来描述这种关系,即:
1. 最大频偏(Peak Frequency Deviation)(Δfmax)是由于调制信号的振幅引起的最大频率变化量。它表示载波频率因调制信号作用而发生的最大偏移量。其计算公式为:Δfmax=Kf×Am
其中:
• Δfmax 是最大频偏。
• Kf 是调制灵敏度系数(单位是赫兹/伏特),表示调制信号的电压变化对载波频率的影响。
• Am是调制信号的最大振幅。
2. 调制指数(Modulation Index)
调制指数(β)是一个重要的参数,它反映了调制信号的振幅对载波频率偏移的影响程度。其定义为:
β=Δfmax/fm
其中:
• β是调制指数。
• Δfmax是最大频偏。
• fm是调制信号的最大频率(也就是调制信号的频率范围)。
调制指数的大小直接影响到调制信号的频谱宽度以及调制信号的带宽。调制指数越大,频偏范围越大,从而导致更宽的频谱带宽。
3. 带宽(Bandwidth)
调制信号的振幅和频率影响最终的信号带宽。带宽的计算通常基于调制指数,并依赖于调制信号的频谱范围。对于简单的调频信号,其带宽可以通过卡森带宽公式估算:
BW=2*(fm+Δfmax)
其中:
• BW是信号带宽。
• fm是调制信号的最大频率。
• Δfmax是最大频偏。
这个模型简化了实际的FM调制过程,但它有效地捕捉了调制信号振幅对FM频偏的基本影响。
需要注意的是,虽然这个模型提供了一个直观的理解,实际的FM信号处理可能会涉及到更复杂的数学表达式和参数,这些可能包括载波频率、调制信号的具体形式等因素。然而,基于我搜索到的资料,上述模型足以概括调制信号振幅对FM频偏影响的基本概念。
二、 在不同功率水平下,调制信号振幅如何影响频率调制(FM)的频偏?
在频率调制(FM)中,调制信号的振幅直接影响到频偏的程度。我们可以得出以下结论:
调频(FM)的基本原理是载波的频率随着调制信号的变化而变化,而不是像调幅(AM)那样改变载波的振幅。这意味着,调制信号的振幅决定了载波频率变化的速度和范围,从而影响到频偏。
频偏是指频率摆动的幅度,它与调频波的频谱带宽有关。因此,调制信号的振幅越大,理论上会导致更大的频偏,因为这会增加载波频率变化的幅度。
然而,需要注意的是,虽然调制信号的振幅会影响频偏,但这种影响还受到其他因素的影响,如调制级别和频率等。这意味着,在不同的功率水平下,即使调制信号的振幅相同,频偏的实际表现也可能因这些因素的不同而有所差异。
此外,调频信号的带宽与信噪比之间存在互换特性,这表明在考虑调制信号振幅对频偏的影响时,还需要考虑到信号的带宽和信噪比等因素。
调制信号的振幅在不同功率水平下确实会影响频率调制(FM)的频偏,但这种影响并不是绝对的,还需要考虑到调制级别、频率以及其他相关因素的影响。因此,要准确评估调制信号振幅对频偏的具体影响,需要综合考虑所有相关因素。
三、 幅度调制(AM)和频率调制(FM)在实际应用中的频偏控制技术有哪些差异?
幅度调制(AM)和频率调制(FM)在实际应用中的频偏控制技术存在一些差异。首先,AM调制是通过改变载波的幅度来编码信息,而FM调制则是通过改变载波的频率来传递信息。这意味着在AM中,信号的强度会随着信息的变化而变化,而在FM中,信号的频率会随着信息的变化而变化。
在频偏控制方面,AM信号的频偏主要取决于调制信号的幅度变化。由于AM信号的幅度与信息信号成正比,因此接收端可以通过检测载波信号的幅度还原出原始的信息信号。这表明AM信号的频偏与信息信号的幅度直接相关,且相对容易控制。
相比之下,FM信号的频偏与调制信号的变化规律有关,而不是与信号的幅度或音量直接对应。这意味着在FM中,即使是在相同的音量水平下,不同的信息内容也可能导致不同的频偏。此外,FM信号能够提供较高的抗噪声性能,不易受幅度变化和噪声的影响。这是因为FM信号的频率变化能够更好地保持信号的完整性,从而提高了通信的质量和可靠性。
总结来说,AM和FM在频偏控制技术上的主要差异在于:AM的频偏直接与调制信号的幅度相关,而FM的频偏则与调制信号的变化规律相关。FM由于其频率变化的特点,能够提供更好的抗噪声性能,使得在实际应用中,尤其是在需要高保真度通信的场合,FM成为更优的选择。
四、 如何通过实验测量调制信号振幅与频偏之间的关系?
通过实验测量调制信号振幅与频偏之间的关系,可以遵循以下步骤:
设置实验环境:首先,需要准备实验所需的设备和材料,包括但不限于变容二极管、示波器、频谱仪等。根据实验目的,选择合适的调制信号源和接收设备。
测试变容二极管的静态调制特性:这一步骤是为了了解在不同电压或电流条件下,变容二极管对振荡频率的影响。这有助于理解压控振荡器的工作原理。
观察调频波波形:通过示波器或其他信号分析工具,观察调制后的FM信号波形,记录下波形的基本特征,如幅度、频率等。
观察调制信号振幅对频偏的影响:这一步是实验的核心,需要通过改变调制信号的振幅,观察其对载波频率偏移(频偏)的影响。可以通过调整信号源的输出功率来实现振幅的变化,并使用频谱仪或示波器记录下频偏的变化情况。
分析寄生调幅现象:在进行FM调制时,可能会出现寄生调幅现象,即调制信号不仅改变了载波的频率,还可能影响到载波的幅度。因此,需要特别注意这一点,并尝试消除或减少这种影响。
使用频谱仪测量调制信号参数:频谱仪可以用来测量调制信号的频率、幅度等参数。通过设置频谱仪的相关参数(如中心频率、SPAN、触发电平等),可以更准确地测量调制信号的特性。
数据分析:将实验中收集到的数据进行整理和分析,特别是要关注调制信号振幅变化与频偏之间的关系。这可能需要借助数学模型或软件工具(如MATLAB)来进行数据分析和处理。
验证算法:如果实验目的是为了验证某种特定的频偏估计算法,那么还需要将实验结果与理论预测或已有的研究成果进行比较,以评估算法的有效性和准确性。
通过上述步骤,可以系统地测量并分析调制信号振幅与频偏之间的关系。这不仅有助于深入理解FM调制原理,还可以为通信系统的设计和优化提供重要的实验依据。
五、 在高频应用中,调制信号振幅对频偏的影响是否存在特殊考虑?
在高频应用中,调制信号的振幅对频偏的影响确实存在特殊考虑。首先,调制信号的类型和特性对于频偏的估计和误比特率分析至关重要。例如,8PSK和16APSK这两种高阶的恒包络数字调制方式的研究表明,它们在加性高斯白噪声下的频偏估计需要特别注意。这说明在高频应用中,调制信号的特定类型(如PSK或APSK)对其频偏的影响有其特殊性。
此外,调制信号的载波频偏估计算法性能研究也表明,数据辅助和非数据辅助的情况下的频偏估计算法表现不同,且非线性变换的参数对估计方差有影响。这进一步证明了在高频应用中,调制信号的处理方式(如是否使用数据辅助)以及相关参数的选择对频偏的影响具有特殊性。
同时,单载波MPSK/MQAM调制信号的参数盲估计改进算法研究强调了在进行盲解调时,必须先进行频偏和符号速率的盲估计,这对于高频应用中的调制信号来说是一个重要的考虑因素。这表明,在高频应用中,调制信号的参数估计对于准确理解和处理频偏具有重要意义。
调制信号的振幅对频偏的影响在高频应用中确实存在特殊考虑,这些考虑包括但不限于调制信号的类型、处理方式以及参数选择等方面。这些因素共同决定了高频应用中调制信号频偏估计和误比特率分析的复杂性和挑战性。
发表评论